The stochastic nonlinear Schrödinger equation is one of the most interesting and influential research directions in the field of partial differential equations in recent decades. Assistant Professor Yue Haitian at IMS with his collaborators have made important progress in this direction. The research results were published in the November 17 issue of Inventiones Mathematicae, one of the four leading mathematical journals in the world. The nonlinear dispersive partial differential equation represented by the Schrödinger equation is a type of partial differential equation describing the dispersion phenomena widely existing in nature, and it can be applied in quantum physics, optics, condensed matter physics, water wave equation, etc.
The stochastic initial value method is a classical approach to mathematically understanding the problem of evolution of regular initial values under nonlinear partial differential equations, while the stochastic initial value problem with low regularity is a central problem in the mathematical verification of Gibbs measure invariance in statistical mechanics. Yue Haitian, together with Professor Deng Yu at the University of Southern California, and Professor Andrea Nahmod at the University of Massachusetts, Amherst, created the random tensor theory, which solves the problem of short time fitness under low regularity random initial values for a class of nonlinear Schrödinger equations with probability subcriticality, and provides an accurate description of the random evolution interactions at different frequencies through the stochastic tensor. The theory is another important advance in this research direction after the progress made by Fields Medalist Simkon Burgan in 1996, and it has strongly promoted the understanding of the evolution structure of random initial values under nonlinear dispersion equations.
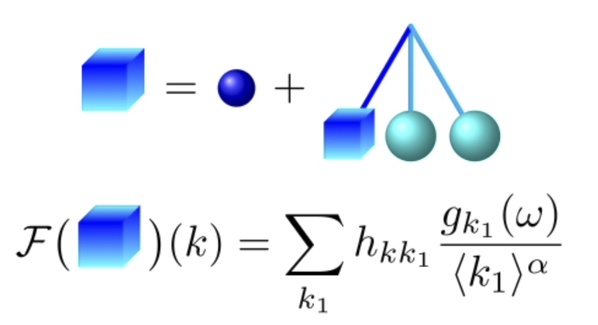
Yue's article is the second paper published in Inventiones Mathematicae by IMS in the last two years. The Founding Director of IMS Chen Xiuxiong commented, Yue Haitian's achievements are encouraging and give me more confidence in achieving the vision of the Institute of Mathematical Sciences.
Link to the article: https://link.springer.com/article/10.1007%2Fs00222-021-01084-8

