近日,上海科技大学物质科学与技术学院拓扑物理实验室刘健鹏课题组在二维人工超晶格体系中的分数拓扑物态方向取得系列进展,相关成果分别发表于国际知名期刊《物理评论快报》(Physical Review Letters)、《自然-材料》(Nature Materials)和《物理评论B》(Physical Review B)。
分数量子霍尔效应是二维电子气体系在强磁场下涌现的一种强关联拓扑物态,其特征表现为量子霍尔电导以e2/h为单位呈现出分数化平台,并具有携带分数电荷的任意子准粒子激发。有些分数量子霍尔态可能衍生出具有非阿贝尔统计的任意子激发,为未来拓扑量子计算的实现奠定了基础。然而,分数量子霍尔效应的实现条件极其苛刻,需要极低温和强磁场。因此,近年来研究人员致力于在无需外磁场的晶格材料中实现类似的物态,并提出了“分数陈绝缘体”以及其他更广义的分数化拓扑物态的概念。
分数陈绝缘体态于2023年首次在转角MoTe2莫尔超晶格中实现,实验上表现出零磁场下的分数化量子霍尔平台,称为分数量子反常霍尔效应。一系列分数量子反常霍尔效应在菱方堆垛的五层石墨烯和氮化硼对齐形成的莫尔超晶格体系中得以实现。菱方多层石墨烯作为一类具备本征非平凡能带拓扑的二维量子材料,在垂直电场调控下可打开能隙并具有非零的贝里曲率和平坦能带。由菱方多层石墨烯形成的人工二维超晶格体系,是探索零磁场关联拓扑物态,尤其是分数化拓扑物态的理想平台。围绕这一方向,刘健鹏课题组近年来开展了系统性的理论研究,取得系列进展。
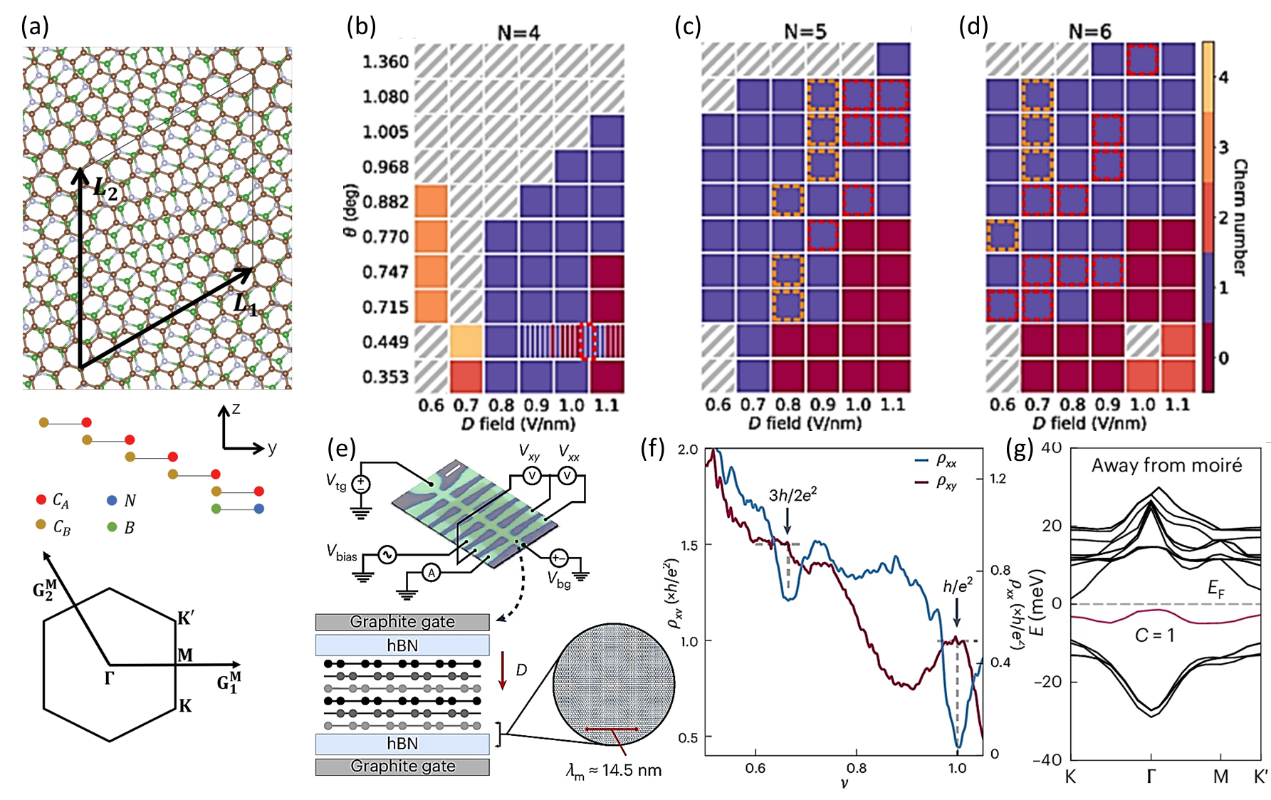
图1:(a) 菱方五层石墨烯-氮化硼莫尔超晶格示意图。(b)-(d) 菱方四层、五层及六层石墨烯的分数陈绝缘体理论相图。虚线红框表示分数陈绝缘体,不同颜色表示平带的陈数。(e) 六层菱方石墨烯-氮化硼莫尔超晶格器件光显照片和示意图。(e) 纵向电阻和霍尔电阻随着填充子的变化。(f) 含有陈数为1平带的能带图。
菱方多层石墨烯/氮化硼莫尔超晶格中的分数陈绝缘体
刘健鹏课题组聚焦于菱方多层石墨烯-氮化硼莫尔超晶格体系 (图1a),发展了一套结合低能有效连续模型、重整化群、自洽电场屏蔽、非约束Hartree-Fock近似与精确对角化的多尺度理论方法。研究发现,在五层石墨烯中,填充数处存在陈数为1的拓扑平带,其在1/3和2/5空穴填充下可分别出现Laughlin型与复合费米子型的分数陈绝缘体,与实验观测完全一致。研究还进一步表明,分数陈绝缘体在四层 (图1b)和六层 (图1d) 菱方石墨烯莫尔超晶格体系中同样可能出现,展现出该拓扑物态在菱方多层石墨烯体系中的普适性。
北京大学卢晓波课题组进一步在六层菱方石墨烯-氮化硼莫尔超晶格体系(图1e)中成功观测到零磁场下的整数量子反常霍尔态(ν=1)与分数陈绝缘体态(ν=2/3)(图1f)。针对这一实验结果,刘健鹏课题组通过理论计算揭示了莫尔超晶格带来的莫尔势和以及电子间强库伦相互作用是产生拓扑平带(图1g),并进一步在平带分数填充下打开拓扑能隙、稳定分数陈绝缘体态的关键。该工作延续并拓展了在上一项工作中建立的理论框架,引证了之前的理论预言,进一步确认菱方多层石墨烯是实现零磁场分数拓扑物态的普适平台。
上述第一项成果以“Fractional Chern insulator states in multilayer graphene moiré superlattices”为题发表于《物理评论B》(Physical Review B),被选为编辑推荐,并被Journal Club for Condensed Matter Physics撰写专题评述。上海科技大学物质学院博士生郭忠青和助理研究员吕昕为共同第一作者,刘健鹏教授为通讯作者。上海科技大学为第一完成单位和通讯单位。第二项成果以“Tunable fractional Chern insulators in rhombohedral graphene superlattices”为题发表于《自然-材料》(Nature Materials)。北京大学量子材料科学中心博士研究生谢键为本文的第一作者,北京大学卢晓波教授与上海科技大学刘健鹏教授为共同通讯作者。
相关论文链接:https://journals.aps.org/prb/abstract/10.1103/PhysRevB.110.075109
https://www.nature.com/articles/s41563-025-02225-7
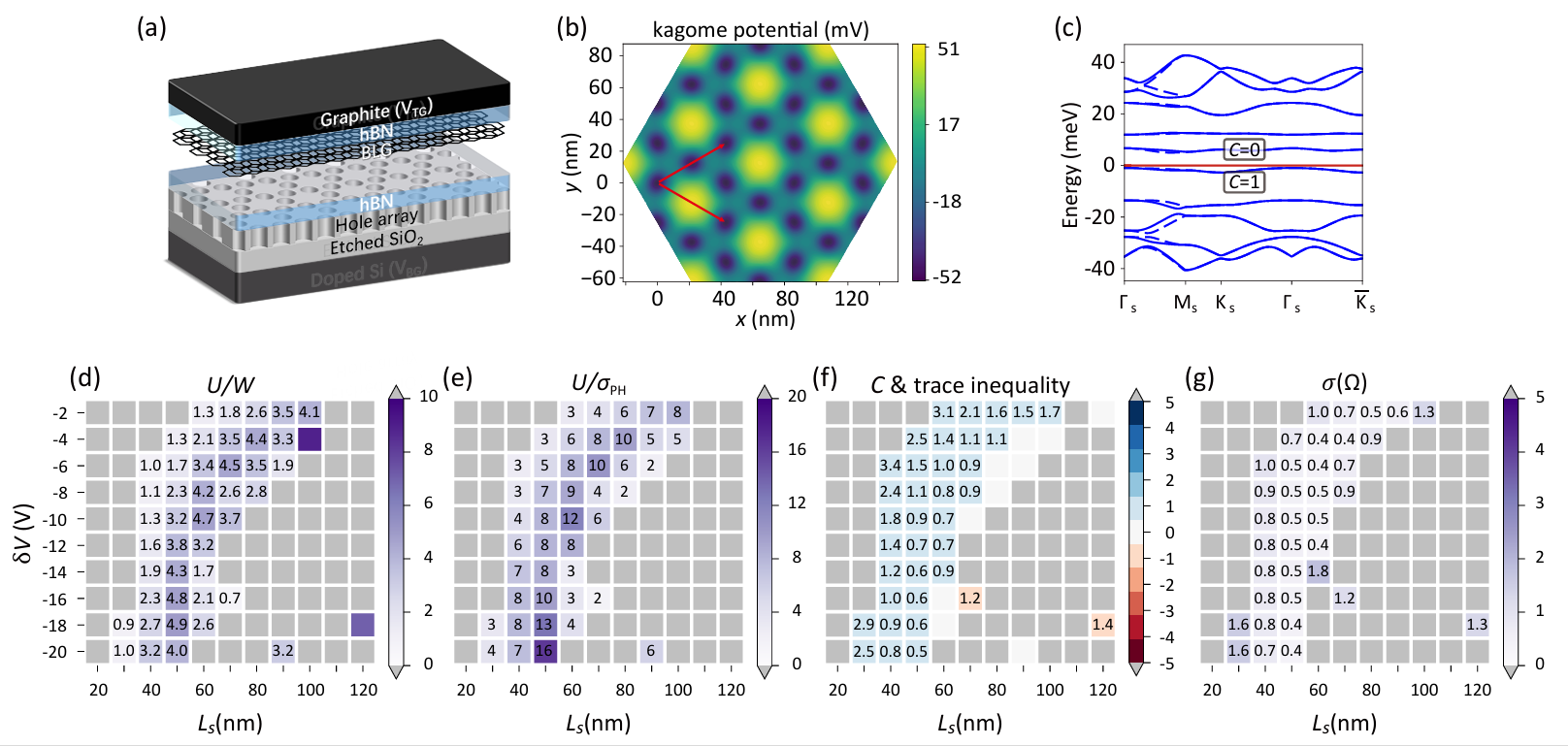
图2:(a) 人工介电超晶格与菱方多层石墨烯耦合器件示意图。(b) 笼目超晶格势。(c) 能带图。(d)相互作用特征强度U和带宽的比值。(e) U和粒子空穴对称性破缺程度的比值。(f) 平带的陈数和量子几何性质。(g) 贝里曲率标准差。
笼目人工介电超晶格与菱方多层石墨烯耦合体系中的分数化拓扑物态
分数陈绝缘体的实现要求体系具有类似朗道能级的拓扑非平庸且量子几何性质良好的平带。传统实现方案主要依赖层间转角形成的莫尔超晶格,这类体系对“魔角”精度极为敏感,且易受转角不均匀性和不可控的晶格弛豫的影响。为突破这一瓶颈,刘健鹏课题组提出了一种无需转角、灵活可调控的用于研究分数拓扑物态的新平台:将菱方多层石墨烯转移至预图案化的二氧化硅衬底上,该衬底表面蚀刻有周期性排列的笼目纳米孔阵列 (图2a)。通过施加独立的顶栅与底栅电压,可在石墨烯中诱导出笼目超晶格势 (图2b)。
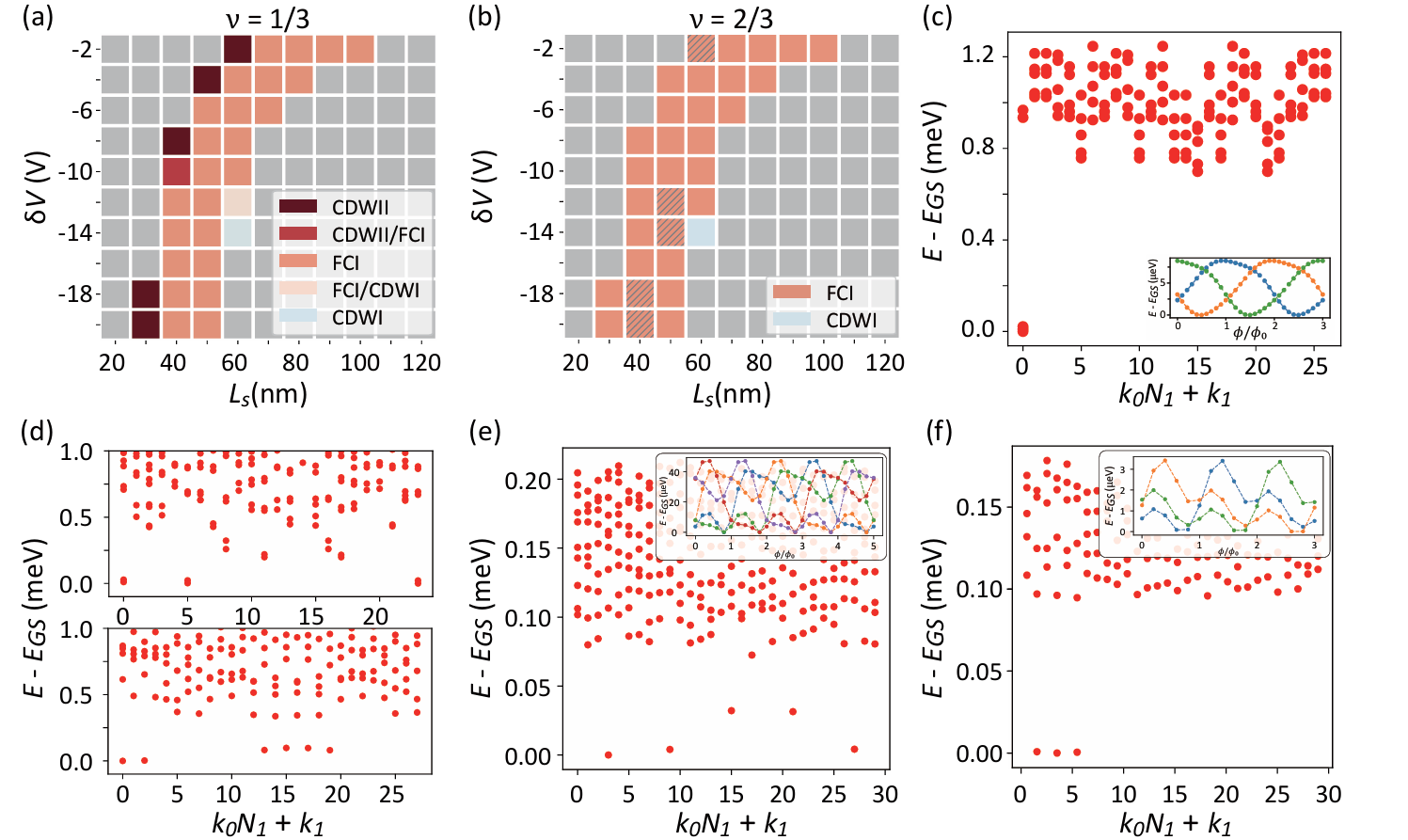
图3:(a) 1/3电子填充基态相图。(b) 2/3电子填充基态相图。(c) 分数陈绝缘体态能谱。(d) 复合费米液体能谱。(e-f) Halperin 型分数陈绝缘体能谱。
基于这一新平台,团队构建了精确的低能有效连续模型,并在超晶格周期Ls与栅压差δV构成的参数空间中,系统研究了体系的单粒子能带结构、拓扑和量子几何性质,以及粒子–空穴对称性破缺程度 (图2d-g)。计算表明,通过调控笼目超晶格周期Ls以及顶栅和底栅的电压差δV,该体系能在Ls∈[40 nm,100 nm],δV ∈[-20 V,-2 V] 的参数范围内生成近乎理想的拓扑平带 (图2c)。在此基础上,课题组进一步采用精确对角化方法研究了平带在分数填充下的多体基态。结果发现:在1/3和2/3填充时体系基态符合分数陈绝缘体的典型特征 (图3a-c);在1/2填充时体系的基态则出现复合费米液体行为 (图3d)。特别在菱方三层石墨烯的高陈数(C = 2)平带中,理论进一步预言了可能存在Halperin 型分数陈绝缘体态 (图3e-f)。
这项工作为实现高度可控、鲁棒性强的零磁场分数拓扑物态提供了全新的理论平台与实验思路。该成果以“Fractional topological states in rhombohedral multilayer graphene modulated by kagome superlattice”为题发表于《物理评论快报》(Physical Review Letters),并被选为编辑推荐。上海科技大学物质学院2022级博士生石嫣然为第一作者,博士生解博、郭忠青、助理研究员吕昕为共同作者,刘健鹏教授为通讯作者。合作者包括上海科技大学柳仲楷教授以及美国Flatiron研究所计算量子物理研究中心Nicolas Regnault教授。上海科技大学为第一完成单位和通讯单位。
论文链接:https://journals.aps.org/prl/abstract/10.1103/21vs-prpj


 沪公网安备 31011502006855号
沪公网安备 31011502006855号